[자료구조] 그래프(graph)

그래프

## 그래프 (Graph) 란?

• 그래프는 실제 세계의 현상이나 사물을 정점(Vertex) 또는 노드(Node) 와 간선(Edge)로 표현하기 위해 사용

관련 용어

• 노드 (Node): 위치를 말함, 정점(Vertex)라고도 함
• 간선 (Edge): 위치 간의 관계를 표시한 선으로 노드를 연결한 선이라고 보면 됨 (link 또는 branch 라고도 함)
• 인접 정점 (Adjacent Vertex) : 간선으로 직접 연결된 정점(또는 노드)

그래프 (Graph) 종류

무방향 그래프 (Undirected Graph)

• 방향이 없는 그래프

• 간선을 통해, 노드는 양방향으로 갈 수 있음

• 보통 노드 A, B가 연결되어 있을 경우, (A, B) 또는 (B, A) 로 표기

  <img src="https://www.fun-coding.org/00_Images/undirectedgraph.png" alt="img" style="zoom:33%;" />
  

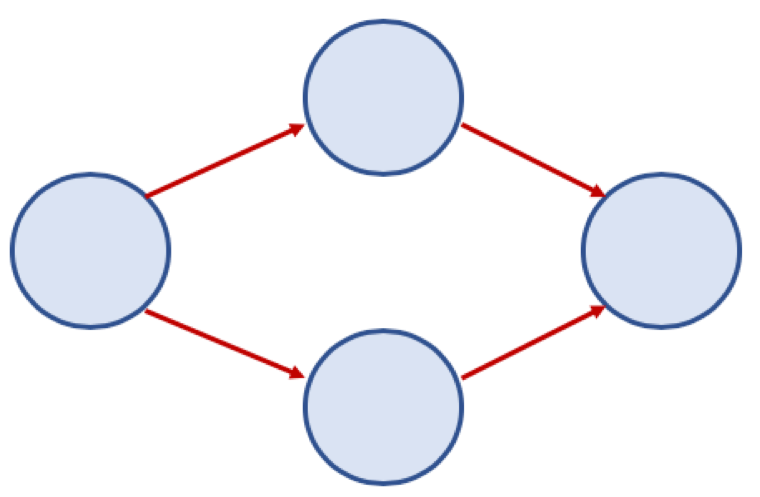
방향 그래프 (Directed Graph)

• 간선에 방향이 있는 그래프
• 보통 노드 A, B가 A -> B 로 가는 간선으로 연결되어 있을 경우, <A, B> 로 표기 (<B, A> 는 B -> A 로 가는 간선이 있는 경우이므로 <A, B> 와 다름)

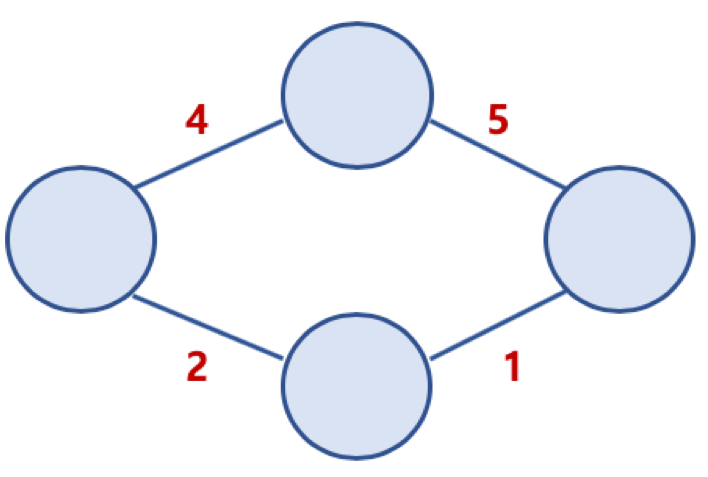
가중치 그래프 (Weighted Graph) 또는 네트워크 (Network)

• 간선에 비용 또는 가중치가 할당된 그래프

  

그래프와 트리의 차이

	그래프	트리
정의	노드와 노드를 연결하는 간선으로 표현되는 자료 구조	그래프의 한 종류, 방향성이 있는 비순환 그래프
방향성	방향 그래프, 무방향 그래프 둘다 존재함	방향 그래프만 존재함
사이클	사이클 가능함, 순환 및 비순환 그래프 모두 존재함	비순환 그래프로 사이클이 존재하지 않음
루트 노드	루트 노드 존재하지 않음	루트 노드 존재함
부모/자식 관계	부모 자식 개념이 존재하지 않음	부모 자식 관계가 존재함

---

파이썬으로 그래프를 표현

# 인접 그래프 예시

graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

print(graph)

---------------------

{'A': ['B', 'C'],
 'B': ['A', 'D'],
 'C': ['A', 'G', 'H', 'I'],
 'D': ['B', 'E', 'F'],
 'E': ['D'],
 'F': ['D'],
 'G': ['C'],
 'H': ['C'],
 'I': ['C', 'J'],
 'J': ['I']}

# 인접 행렬 예시

class Graph():
    def __init__(self, size):
        self.SIZE = size
        self.graph = [[0 for _ in range(size)] for _ in range(size)]

A, B, C, D = 0, 1, 2, 3

G = Graph(4) # 4x4 2차원 배열의 그래프
G.graph[A][B] = 1
G.graph[A][C] = 1
G.graph[A][D] = 1
G.graph[B][A] = 1
G.graph[B][C] = 1
G.graph[C][D] = 1
G.graph[C][A] = 1
G.graph[C][B] = 1
G.graph[D][A] = 1
G.graph[D][C] = 1


for i in range(4):
    for j in range(4):
        print(G.graph[i][j], end=' ')
    print()
    
-----------------------------

>>> 0 1 1 1 
    1 0 1 0
    1 1 0 1
    1 0 1 0

인접 리스트 vs 인접 행렬

• 노드의 개수 : V (Vertex)
• 엣지의 개수 : E (Edge)

노드 수가 V 일 때, 그래프 안에는 최대 V^2 개의 Edge가 들어갈 수 있다.

차지하는 공간

인접행렬은 V x V의 행렬이므로 V^2의 공간을 차지

인접리스트는 노드를 저장하는 공간 V + 노드마다 포함된 엣지를 저장하는 공간 E, 총 V+E

연결됐는지 확인하는데 걸리는 시간

인접 행렬은 두 노드가 인접했는지 아닌지 O(1)로 확인 (matrix[3][5] 같은 방식)

인접 리스트는 한 노드의 리스트 안에 특정 역이 저장됐는지를 탐색하므로, 최소 O(1) 최대 O(V)

한 노드에 연결된 모든 시간을 확인

인접 행렬은 그 노드의 배열(혹은 행)을 전부 살펴야 하므로 O(V)

인접 리스트는 인접 노드의 래퍼런스를 가지고 있으므로 최소 O(1), 최대(모든 노드와 연결되있는 경우) O(V)

	인접행렬	인접리스트
차지하는 공간	O(V^2)	O(V+E)
연결 확인	O(1)	O(1)~O(V)
연결 노드 전체 탐색	O(V)	O(1)~O(V)

대체로 인접 리스트를 사용하는 것이 좀 더 효율적이다.